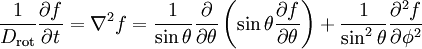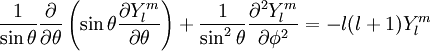Rotational diffusion

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Rotational diffusion is a process by which the equilibrium statistical distribution of the overall orientation of particles or molecules is maintained or restored. Rotational diffusion is the counterpart of translational diffusion, which maintains or restores the equilibrium statistical distribution of particles' position in space.

The random re-orientation of molecules (or larger systems) is an important process for many biophysical probes. Due to the equipartition theorem, larger molecules re-orient more slowly than do smaller objects and, hence, measurements of the rotational diffusion constants can give insight into the overall mass and its distribution within an object. Quantitatively, the mean square of the angular velocity about each of an object's principal axes is inversely proportional to its moment of inertia about that axis. Therefore, there should be three rotational diffusion constants - the eigenvalues of the rotational diffusion tensor - resulting in five rotational time constants [1][2]. If two eigenvalues of the diffusion tensor are equal, the particle diffuses as a spheroid with two unique diffusion rates and three time constants. And if all eigenvalues are the same, the particle diffuses as a sphere with one time constant. The diffusion tensor may be determined from the Perrin friction factors, in analogy with the Einstein relation of translational diffusion, but often this is inaccurate and direct measurement is required.

The rotational diffusion tensor may be determined experimentally through fluorescence anisotropy, flow birefringence, dielectric spectroscopy, NMR relaxation and other biophysical methods sensitive to picosecond or slower rotational processes. In some techniques such as fluorescence it may be very difficult to characterize the full diffusion tensor, for example measuring two diffusion rates can sometimes be possible when there is a great difference between them, e.g., for very long, thin ellipsoids such as certain viruses. This is however not the case of the extremely sensitive, atomic resolution technique of NMR relaxation that can be used to fully determine the rotational diffusion tensor to very high precision.

Contents

[edit] Basic equations of rotational diffusion

For rotational diffusion about a single axis, the mean-square angular deviation in time t is

langletheta^2rangle = 2 D_r t !

where Dr is the rotational diffusion coefficient (in units of radians2/s). The angular drift velocity Ωd = (dθ / dt)drift in response to an external torque Γθ (assuming that the flow stays non-turbulent and that inertial effects can be neglected) is given by

Omega_d = frac{Gamma_theta}{f_r}

where fr is the frictional drag coefficient. The relationship between the rotational diffusion coefficient and the rotational frictional drag coefficient is given by the Einstein relation (or Einstein–Smoluchowski relation):

D_r = frac{k_B T}{f_r}

where kB is the Boltzmann constant and T is the absolute temperature. These relationship are in complete analogy to translational diffusion.

The rotational frictional drag coefficient for a sphere of radius R is

f_{r, textrm{sphere}} = 8 pi eta R^3 ! where η is the dynamic viscosity.

[edit] Rotational version of Fick's law

A rotational version of Fick's law of diffusion can be defined. Let each rotating molecule be associated with a vector n of unit length n·n=1; for example, n might represent the orientation of an electric or magnetic dipole moment. Let f(θ, φ, t) represent the probability density distribution for the orientation of n at time t. Here, θ and φ represent the spherical angles, with θ being the polar angle between n and the z-axis and φ being the azimuthal angle of n in the x-y plane. The rotational version of Fick's law states

frac{1}{D_{mathrm{rot}}} frac{partial f}{partial t} = nabla^{2} f = frac{1}{sintheta} frac{partial}{partial theta}left( sintheta frac{partial f}{partial theta} right) + frac{1}{sin^{2} theta} frac{partial^{2} f}{partial phi^{2}}

This partial differential equation (PDE) may be solved by expanding f(θ, φ, t) in spherical harmonics for which the mathematical identity holds

frac{1}{sintheta} frac{partial}{partial theta}left( sintheta frac{partial Y^{m}_{l}}{partial theta} right) + frac{1}{sin^{2} theta} frac{partial^{2} Y^{m}_{l}}{partial phi^{2}} = -l(l+1) Y^{m}_{l}

Thus, the solution of the PDE may be written

f(theta, phi, t) = sum_{l=0}^{infty} sum_{m=-l}^{l} C_{lm} Y^{m}_{l}(theta, phi) e^{-t/tau_{l}}

where Clm are constants fitted to the initial distribution and the time constants equal

tau_{l} = frac{1}{D_{mathrm{rot}}l(l+1)}

[edit] See also

[edit] Notes and references

  1. ^ Perrin, Francis (1934). "Mouvement brownien d'un ellipsoide (I). Dispersion diélectrique pour des molécules ellipsoidales". Le Journal de Physique 7 (5): 497–511. 
  2. ^ Perrin, Francis (1936). "Mouvement brownien d'un ellipsoide (II). Rotation libre et dépolarisation des fluorescences: Translation et diffusion de molécules ellipsoidales". Le Journal de Physique 7 (7): 1–11. 

[edit] Further reading

  • Cantor, CR; Schimmel PR (1980). Biophysical Chemistry. Part II. Techniques for the study of biological structure and function. W. H. Freeman. 
  • Berg, Howard C. (1993). Random Walks in Biology. Princeton University Press. 
Retrieved from "http://en.wikipedia.org/wiki/Rotational_diffusion"