Christofides algorithm
The goal of the Christofides approximation algorithm (named after Nicos Christofides) is to find a solution to the instances of the traveling salesman problem where the edge weights satisfy the triangle inequality. Let 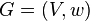 be an instance of TSP, i.e.
be an instance of TSP, i.e.  is a complete graph on the set
is a complete graph on the set 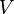 of vertices with weight function
of vertices with weight function 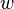 assigning a nonnegative real weight to every edge of
assigning a nonnegative real weight to every edge of  .
.
Contents
[hide]Algorithm[edit]
In pseudo-code:
- Create a minimum spanning tree
 of
of  .
. - Let
 be the set of vertices with odd degree in
be the set of vertices with odd degree in  and find a perfect matching
and find a perfect matching  with minimum weight in the complete graph over the vertices from
with minimum weight in the complete graph over the vertices from  .
. - Combine the edges of
 and
and  to form a multigraph
to form a multigraph  .
. - Form an Eulerian circuit in
 (H is Eulerian because it is connected, with only even-degree vertices).
(H is Eulerian because it is connected, with only even-degree vertices). - Make the circuit found in previous step Hamiltonian by skipping visited nodes (shortcutting).
Approximation ratio[edit]
The cost of the solution produced by the algorithm is within 3/2 of the optimum.
The proof is as follows:
Let A denote the edge set of the optimal solution of TSP for G. Because (V,A) is connected, it contains some spanning tree T and thus w(A) ≥ w(T). Further let  denote the edge set of the optimal solution of TSP for the complete graph over vertices from
denote the edge set of the optimal solution of TSP for the complete graph over vertices from  . Because the edge weights are triangular (so visiting more nodes cannot reduce total cost), we know that w(A) ≥ w(B). We show that there is a perfect matching of vertices from
. Because the edge weights are triangular (so visiting more nodes cannot reduce total cost), we know that w(A) ≥ w(B). We show that there is a perfect matching of vertices from  with weight under w(B)/2 ≤ w(A)/2 and therefore we have the same upper bound for
with weight under w(B)/2 ≤ w(A)/2 and therefore we have the same upper bound for  (because
(because  is a perfect matching of minimum cost). Because
is a perfect matching of minimum cost). Because  must contain an even number of vertices, a perfect matching exists. Let e1,...,e2k be the (only) Eulerian path in
must contain an even number of vertices, a perfect matching exists. Let e1,...,e2k be the (only) Eulerian path in  . Clearly both e1,e3,...,e2k-1 and e2,e4,...,e2k are perfect matchings and the weight of at least one of them is less than or equal to w(B)/2. Thus w(M)+w(T) ≤ w(A) + w(A)/2 and from the triangle inequality it follows that the algorithm is 3/2-approximative.
. Clearly both e1,e3,...,e2k-1 and e2,e4,...,e2k are perfect matchings and the weight of at least one of them is less than or equal to w(B)/2. Thus w(M)+w(T) ≤ w(A) + w(A)/2 and from the triangle inequality it follows that the algorithm is 3/2-approximative.
Example[edit]
 |
Given: metric graph 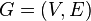 with edge weights with edge weights |
 |
Calculate minimum spanning tree  . . |
 |
Calculate the set of vertices  with odd degree in with odd degree in  . . |
 |
Reduce  to the vertices of to the vertices of  ( (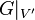 ). ). |
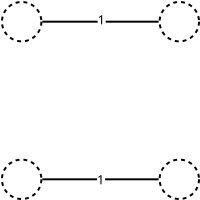 |
Calculate matching  with minimum weight in with minimum weight in 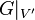 . . |
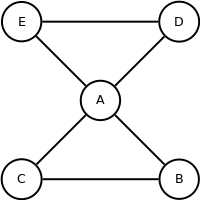 |
Unite matching and spanning tree ( ). ). |
 |
Calculate Euler tour on  (A-B-C-A-D-E-A). (A-B-C-A-D-E-A). |
 |
Remove reoccuring vertices and replace by direct connections (A-B-C-D-E-A). In metric graphs, this step can not lengthen the tour.
This tour is the algorithm's output. |
References[edit]
- NIST Christofides Algorithm Definition
- Nicos Christofides, Worst-case analysis of a new heuristic for the travelling salesman problem, Report 388, Graduate School of Industrial Administration, CMU, 1976.
 .
.