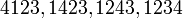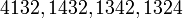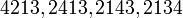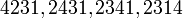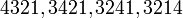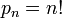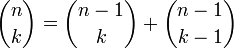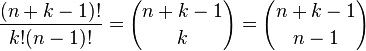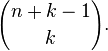Kombinatorika

December 18, 2011 | Author exprescimi

Kombinatorika

Kombinatorika merret me studimin e bashkësive të fundme, me grupimin e elementeve të tyre sipas ndonjë kriteri të caktuar, me renditjen e elementeve etj. Kuptimet themelore të kombinatorikës janë permutacioni, kombinacioni, variacioni, multibashkësia etj. . Ajo është e lidhur ngushtë me degë tjera të matematikës si Algjebra, Teoria e gjasës, dhe Gjeometria, dhe ka zbatime të shumta në Shkencat kompujterike në Statistikë etj. Aspekte të kombinatorikës konsistojnë në llogaritjen e numrit të objekteve të cilat plotësojnë ndonjë kriter të caktuar përbën objektin e studimit të Kombinatorikës numerike, Gjetjen e elementit ose objektit më të madh ose më të vogël ose zgjedhjen optimale këto probleme i studjonKombinatorika ekstrmale, poashtu zhvillimi dhe gjetja e strukturave të cilat i plotësojnë objektet kombinatorike, i studjon Kombinatorika algjebrike.

Kombinatorika më shumë merret me zgjidhjen e problemeve se me ndërtimin e një teorie, por kjo nuk do të thotë se gjatë këtij zhvillimi nuk është ndërtuar një teori e fuqishme e kombinatorikës sidomos në fund të shekullit XX . Njëra nga pjesët e kombinatorikës është edhe Teoria e grafeve.

Matematikani i cili është i specializuar në kombinatorikë quhet kombinatorist.

Historia e kombinatorikës

Gjurmë të kombinatorikës gjejmë te Xhainistët në Indi, matematikani Pingala e zbuloi metodën e përcaktimit të numrit të kombinacioneve të një numri të dhënë shkronjash, prej të cilave zgjedhim 1, 2, etj. Mahavira rreth vitit 850 i dha formulat e përgjithshme për gjetjen e numrit të permutacioneve dhe kombinacioneve të një bashkësie të fundme. Bhaskaracharya për kombinatorikën përdorte emërtimin Anka Pasha në Lilavati. Ai dha disa formula të reja në kombinatorikë. ^[1] Disa arritje të rëndësishme janë dhënë nga grekët e vjetër dhe kinezët. Disa matematikan arab dhe çifut kanë përdorur konceptet e permutacionit dhe kombinacionit gjatë vështrimeve astronomike p.sh. Rabbi ben Ezra rreth vitit 1140). Libri i parë modern i shkruajtur me subjekt kombinatorikën është Ars Conjectandi i shkruajtur nga matematikani i shquar Jacob Bernoulli i cili u botua në vitin 1713.

Kombinatorika numerike

Kombinatorika numerike është fusha më klasike e kombinatorikës, ajo merret me llogaritjen e numrit të konfiguracioneve të cilat përkufizohen nga elementet e një bashkësie të caktuar objektesh. Shumica e problemeve të cilat hasen në kombinatorikën numerike kanë formulim të thjeshtë kombinatorik p.sh disa prej tyre janë Numrat e Fibonaccit, Numrat e Catalanit, Numri i permutacioneve, kombinacioneve, Particioni i numrit natyral Particioni i bashkësisë, Kompozicioni i numrit natyral etj.

Kombinatorika analitike

Kombinatorika analitike merret me studimin e strukturave kombinatorike duke shfrytëzuar konceptet nga Analiza komplekse dhe nga Teoria e gjasës. Përderisa kombinatorika numerike nxjer formula eksplicite duke i shfrytëzuar p.sh funksionet gjeneratrisa kombinatorika analitike përfundimet i jep me formula asimptotike.

Numrat e Fibonaccit

Numra të Fibonaccit janë termat e vargut të pafundëm të numrave natyral i cili fillon me 0 dhe ç'do term tjetër është shumë e dy termave parardhëss. Me fjalë tjera termat e këtij vargu e plotësojnë relacionin rekurent:

$F_n = \begin{cases} 0 & \mbox{: } n = 0; \\ 1 & \mbox{: } n = 1; \\ F_{n-1}+F_{n-2} & \mbox{: } n > 1. \\ \end{cases}$

Njëzet termat e para të vargut të numrave të Fibonaccit janë dhënë në tabelë

F₀	F₁	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F₉	F₁₀	F₁₁	F₁₂	F₁₃	F₁₄	F₁₅	F₁₆	F₁₇	F₁₈	F₁₉	F₂₀
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765

Ç'do i treti numër është tek.

Këta numra emrin e kanë marrë sipas Leonardos nga Pisa, i njohur si Fibonacci, edhepse për ta ka pasur njohuri në Indi shumë më herët.

Permutacioni

Nga Wikipedia, enciklopedia e lirë

Permutacion i një bashkësie të fundme quhet çdo renditje e të gjitha elementeve të saj në varg. Për shembull të gjitha permutacionet e bashkësisë A={1,2,3} janë:

$123,132,213,231,312,321\,$

Shohim se kjo bashkësi ka gjithsejt 6 permutacione. Ngjajshëm vërejmë se bashkësia me 4 elemente $B=\{1,2,3,4\}\,$ ka 4 herë më shumë permutacione se bashkësia A sepse lehtë vërejmë se çdo permutacion i A gjeneron 4 permutacione të B ashtuqë elementin 4 e vendosim në fillim, në mes dy elementeve të para, në mes elementit të dytë dhe elementit të tretë ose në fund të vargut gjegjësisht permutacionit të baashkësisë A. Në këtë mënyrë permutacioni 123 i A gjeneron këto 4 permutacione të B

$4123,1423,1243,1234\,$

permutacioni 132 i A gjeneron këto 4 permutacione të B

$4132,1432,1342,1324\,$

permutacioni 213 i A gjeneron këto 4 permutacione të B

$4213,2413,2143,2134\,$

permutacioni 231 i A gjeneron këto 4 permutacione të B

$4231,2431,2341,2314\,$

permutacioni 312 i A gjeneron këto 4 permutacione të B

$4312,3412,3142,3124\,$

dhe në fund permutacioni 321 i A gjeneron këto 4 permutacione të B

$4321,3421,3241,3214\,$

Numri i permutacioneve

Le të jetë dhënë një bashkësi me $n\,$ elementeatëherë me $p_n\,$ e shënojmë numrin e permutacioneve të saj. Do të do të tregojmë se

$p_n=n!\,$

Për të konstruktuar një permutacion ka $n\,$ mënyra të ndryshme për të zgjedhur elementin e parë. Pas zgjedhjes së tij mbeten, 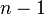$n-1\,$ elemente prej të cilave zgjedhim një dhe e vendosim në vendin e dytë në 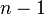$n-1\,$ mënyra. Kështu për vendosjen e dy elementeve të para ekzistojnë gjithsejt

$n(n-1)\,$ mënyra.

Për zgjedhjen e elementit të tretë mbesin 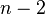$n-2\,$ elemente, prandaj me plotësimin e tre vendeve të para fitohen,

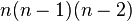$n(n-1)(n-2)\,$ permutacione.

Duke vazhduar në këtë mënyrë derisa të mbeten dy elemente të pazgjedhur për të cilat mbeten 2 mundësi, në fund mbetet një element praandaj për numrin e të gjitha permutacioneve prej $n\,$ elementesh e fitojmë formulën gjegjësisht numrin

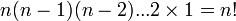$n(n-1)(n-2)...2\times 1=n!\,$ .

Kombinacioni

Kombinacioni është njëri prej kuptimeve themelore të kombinatorikës.

Përkufizim: Ç'do nënbashkësi me k elemente e zgjedhur nga një bashkësi me n elemente quhet kombinacion pa përsëritje i klasës “k” prej “n” elementesh. P.sh të gjitha kombinimet e klasës së tretë të bashkësisë A={a,b,c,d} janë: (a,b,c), {a,b,d}, (a,c,d), (b,c,d} Problem kryesor në lidhje me kombinacionet është gjetja e numrit të tyre. Numrin e kombinacioneve të klasës k prej n elementesh e shënojmë me 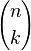${n\choose k}$

Ky numër mund të njehsohet sipas formulës së mëposhtme: 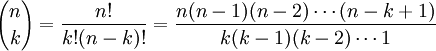${n\choose k}=\frac{n!}{k!(n-k)!}=\frac{n(n-1)(n-2) \cdots(n-k+1)}{k(k-1)(k-2) \cdots1}$

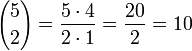
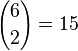
p.sh.: ${5\choose 2}=\frac{5 \cdot4}{2 \cdot1}=\frac{20}{2}=10$ ${6\choose 2}={15}$

Trekëndëshi i Pascalit

Trekëndëshi i Pascalit i jep vlerat e numrit të kombinacioneve, ky trekëndësh në të shumtën e rasteve jepet në trajtën e një trekëndëshi barabrinjës. Ne këtu e kemi dhënë në trajtën e një trekëndëshi kënddrejt numrash sipas rrjeshtave n dhe sipas kolonave k. Në prerjen e rrjeshtit n me kolonën k e vendosim numrin $\binom{n}{k}$ . Duke u bazuar në formulën e tanishme

$\binom{n}{k}=\binom{n-1}{k} + \binom{n-1}{k-1}\,$

e cila tregon se ç'do element i tabelës i cili nuk i takon rreshtit të parë ose kolonës së parë është i barabartë me shumën e elementit mbi të dhe e fqiut të tij të majtë.

Numri i kombinacioneve me përsëritje

Ky numër mund të llogaritet si vijon :

${{(n + k - 1)!} \over {k!(n - 1)!}} = {{n + k - 1} \choose {k}} = {{n + k - 1} \choose {n - 1}}$

p.sh nëse kemi 10 objekteve zgjedhim 3 atëherë (10 + 3 − 1)!/(3!(10 − 1)! = 220 mënyra zgjedhjeje<end>.

Kjo mund të spjegohet kështu. Supozojmë se kemi n + k kuti të njëjta të renditura në vijë. Prej këtyre kutive(përveç të parës), rastësisht zgjedhim k prej tyre dhe kutinë e zgjedhur e kuptojmë si të zbrazët. Kutitë e mbetura mund të plotësohen me n elemente nga bashkësia S. Për ç'do kuti jo të zbrazët e cila pasohet nga M kuti të zbrazëta, ne zgjedhim elementin përkatës nga kutia jo e zbrazët M herë. Si përfundim, ç'do renditje apo zgjedhje e kutisë së zbrazët i përket një zgjedhje e kelementeve prej n elementeve prej të cilave disa ose të gjitha mund të përsëriten. Pra numri i kombinacioneve me përsëritje është:

${n+k-1 \choose k}.$

Algjebra

Algjebra studion strukturat algjebrike (Grupet, Unazat, Trupat, Hapsirat vektoriale, etj.). Me ndihmën e saj bëhet zgjidhja e Ekuacioneve dhe sistemeve të Ekuacioneve. Në algjebren lineare shqyrtohen Matricat dhe Detirminantet. Në teorinë e Galois-it, bëhet shqyrtimi i problemeve gjeometrike në mënyrë algjebrike.

Numrat

Numrat natyror : Prej 1 deri $\infty$ (Infinit/Pafund)

Numrat real dhe vetitë tyre

Vlera absolute e numrave real

Rrethina e pikës

Numrat e përafërt (aproksiomativ)

Numrat e plotë

Numrat iracional

Numrat pozitiv : Numrat me te medhenj se 0

Numrat negativ : Numrat me te vegjel se 0

Numrat kompleks

Barazia e numrave kompleks

Mbledhja dhe shumëzimi i numrave kompleks

Format e numrave kompleks

Forma algjebrike : z = a + bi

Forma trigonomtrike : z = cosϕ + isinϕ

Forma eksponenciale : z = e^iϕ

Veprimi me numra kompleks

Mbledhja dhe zbritja e numrave kompleks

Shumëzimi dhe pjestimi i numrave komples

Fuqizimi i numrave kompleks

Formula e Muavrit : (cosϕ + isinϕ)ⁿ = cosnϕ + isinnϕ

Rrënjëzimi i numrave kompleks

Zgjidhja trigonometike e ekuacionit binomial

Mahavira

Mahavira

Mahavira (Sanskritisht महावीर dhe në gjuhën Tamile அருகன்("Arugan") që do të thotë "Hero i Madh", tradicionalisht 599 – 527 p.r.l.k) është emri që zakonisht lidhet me të urtin indian Vardhamana (Sanskritisht: वर्धमान "duke u rritur") që themeloi ato që janë sot parimet qendrore të Jainizmit. Sipas traditës së Jainit, ai ishte Tirthankara i 24-t dhe i fundit>th. Në gjuhën Tamile, ai quhej Arugan ose Arugadevan. Ai ishte gjithashtu i njohur në tekste si Vira ose Viraprabhu, Sanmati, Ativira,dhe Gnatputra. Në shkrimet budiste Pali Canon, ai quhet Nigantha Nātaputta.

Lindja e Princit Vardhaman

Skeda:Queen Trishala Dream.JPG

Mbretërersha Trishala dhe katëmbëdhjetë ëndrat e saj

Në një vend të quajtur Kshatriyakunda në mbretërinë e lashtë të Lachuar në Distriktin Jamui në Biharin (qytet në Indi) e ditëve të sotme, Mahavira u lind nga Mbreti Siddartha dhe Mbretëresha Trishala më 12 Prill sipas kalendarit Gregorian. Kur akoma qe në barkun e mamasë, besohej se ai i sillte pasuri dhe begati gjithë mbretërisë, për këtë arsye ai u quajt Vardhaman. Mbretëresha Trishala pati 14 ëndrra të mbara para se të lindte Vardhamanin, shenja që profetizonin ardhjen e një shpirti të madh.

Tradita jainiste thoshte se pas lindjes së tij, Indra e la në një vaskë të mbushur me qumësht të hyjnive dhe i kreu ritualet për Tirthankar-in e ardshëm dhe më pas iu kthye mamasë së vet, Trishalës.

Ditëlindja e Vardhamanit festohet në Mahavir Jayanti, festa më e rëndësishme fetare e jainistëve kudo në botë.

Vitet e para

Si djali i Mbretit Siddartha, ai jetoi si një princ. Gjithsesi, edhe në moshë të vogël ai shfaqi një natyrë të virtytshme. Ai filloi të angazhohej në meditime dhe u zhyt në mendime. Ai ishte i interesuar në besimet kryesore të Jainizmit dhe filloi të distancojë veten nga çështjet e rëndomta.

Kërkimi shpirtëror

India në kohën e Mahavirës

Në moshën tridhjetë vjeçare, Mahavira hoqi dorë nga mbretëria dhe familja, la gjithë zotërimet dhe shpenzoi dymbëdhjetë vjet si asket. Gjatë këtyre dymbëdhjetë vjetëve ai e shpenzoi shumicën e kohës duke medituar. Ai dha vlerësimin më të madh për qeniet e tjera, përfshirë njerëzit, kafshët dhe bimët dhe shmangu dëmtimin e tyre. Ai kishte hequr dorë nga gjithë zotërmiet përfshirë dhe rrobat dhe jetoi me një regjim shumë të rreptë. Ai shfaqi kontroll ndaj shqisave të tij kur duronte ndëshkimin e vetvetes gjatë këtyre vjetëve. Kurajoja dhe trimëria e tij i dhanë atij emrin Mahavira. Këto ishin vitet e arta të udhëtimit të tij shpirtëror, në fund të së cilës ai arriti Kaivalya Gyan. Ai tani ishte një person me harmoni, njohuri dhe vetë-kontroll të pafundëm.

Vitet e mëvonshme

Mahavira ia përkushtoi pjesën tjetër të jetës predikimit për liri shpirtërore për njerëzit rreth e rrotull Indisë. Ai udhëtoi zbathur dhe pa rroba, në kushtet më të vështira klimaterike dhe njerëz nga gjithë situata e jetës vinin për të dëgjuar mesazhin e tij. Gjatë një pike Mahavira kishte 400,000 ndjekës. Predikimet dhe përpjekjet e Mahavirës për të shpërndarë filozofinë jainiste konsiderohen si katalistët e vërtetë që e zgjeruan këtë fe të lashtë në tërë Indinë e më tej.

Në moshën 72 vjeçare dhe 4.5 muajsh, ai arriti Nirvanën (çlirimi nga çdo vuajtje) në një zonë të njohur si Paëapuri në ditën e fundit të kalendarëve jainistë dhe indianë, në Dipavali. Jainistët e festojnë këtë si ditën kur ai arriti çlirimin ose Moksha. Jainistët besojnë se Mahavira jetoi nga 599-527 p.r.l.k, ndonëse disa studiues preferojnë 549-477 p.r.l.k.

Filozofia

Jina, ose Mahavir, si guru në një dorëshkrim ,Gujarat, Indi,rreth 1411

Filozofia e Mahavirës ka tetë principe kryesore – tre janë metafizike dhe pesë janë etike. Objektivi është të ngrenë cilësinë e jetës.

Mahavira predikonte se nga përjetësia, çdo qenie e gjallë (shpirti) është në lidhje me atome karmike të akumuluara nga veprimet e mira dhe të këqija. Në një gjendje iluzioni karmik, individi kërkon kënaqësi të përkohshme dhe iluzive në zotërimet materiale, që janë rrënja e shkaqeve të mendimeve të dhunshme dhe veprimeve si inati, urrejtja, zilia, dhe të tjera. Kjo rezulton në akumulimin e mëtejshëm të karmës.

Për tu çliruar nga vetja, Mahavira mësoi nevojshmërinë e besimit të drejtë (samyak-darshana), njohurisë së drejtë (samyak-gyana), dhe sjelljes së drejtë (samyak-charitra'). Në zemër të sjelljes së drejtë për Jainistët janë pesë betimet e mëdha:

(Ahimsa) – të mos i shkaktosh dëme qenieve të tjera të gjalla;
(Satya) – të thuash vetëm të vërtetën;
(Asteya) – të mos marrësh asgjë që nuk të është dhënë siç duhet;
(Brahmacharya) – të knaqesh jo në kënaqësi sensuale;
(Aparigraha) – të heqësh dorë tërësisht nga njerëzit, vendet dhe gjërat materiale.

Këto betime nuk mund të plotësoheshin pa pranuar filozofinë e jo-absolutzmit (Anekantvada) dhe teorinë e relativitetit (Syādvāda, gjithashtu përkthyer "parashikim i kualifikuar"). Murgjërit dhe murgeshat i përmbahen rreptësisht këtyre betimeve.

Mahavira mësonte se meshkujt dhe femrat janë shpirtëra të barabartë dhe se të dy mund të heqin dorë nga bota për të kërkuar moksh-in ose lumturinë e përjetshme.

Mahavira tërhiqte njerëz nga çdo shtresë, të pasur dhe të varfër, meshkuj dhe femra. Ai i organizoi ndjekësit e tij në katër rende; murg (Sadhu), murgeshë (Sadhvi), laikë (Shravak), dhe laike (Shravika). Kjo lloj renditjeje njihet si Chaturvidh Jain Sangh.

Predikimet e Mahavirës u ruajtën nga dishepujt e tij të menjëhershëm në Agam Sutras (dorëshkrime). Me kalimin e kohës shumë Agam Sutrasjanë humbur, shkatërruar ose ndryshuar. Rreth një mijë vjet pas kohës së Mahavirës, Agam Sutras u shkruajtën në Tadpatri (letra me gjethe palme që përdoreshin atëherë për të bërë libra). Jainistët Swetambar i pranojnë këto sutras si mësime autentike kurse Jainistët Digambar i përdorin ato si referenca.

Jainizmi ekzistonte edhe përpara Mahavirës dhe mësimet e tij bazoheshin në ato të paraardhësve të tij. Kështu që Mahavira ishte më shumë një reformator dhe promovues sesa themelues i një besimi të ri. Ai ndoqi besimet e vendosura mirë të paraardhësit të tij, Tirthankar-it Parshvanath. Megjithatë, Mahavira i riorganizoi parimet filozofike të Jainizmit që të korrespondonin me kohën e tij.

Pak shekuj pas Nirvanës së Mahavirës, sekti fetar jainist (Sangh) u rrit më shumë e u bë më i ndërlikuar. Kishte ndarje në pika të vogla, megjithëse ato nuk ndikonin mbi doktrinat origjinale të Mahavirës. Brezat e mëvonshëm panë fillimin e ritualeve dhe kompleksiteteve që disa i kritikuan që vendosnin Mahavirën dhe Tirthankar-ët e tjerë në fron në mënyrë të ngjashme me hyjnitë hindu.

Kopje e tempullit Pavapuri në Pansara. Mahavira arriti Nirvanën në Pavapuri.

Pjatë që shfaq Mahavirën që pranon Alms-in

Mahavira

Folio nga Kalpasutra (Libri i Rregullave të Shenjta) nga Acharya Bhadrabahu, rreth 1400 p.s.l.k

Ekzistojnë tekste të ndryshme Jainiste që përshkruajnë jetën e Lord Mahavirës. Më e shquara prej tyre është Kalpasutra nga Acharya Bhadrabahu I. Biografia e parë sanskrite e Mahavirës ishteVardhamacharitra nga Asaga më 853 p.s.l.k. ^[3]

Shih gjithashtu: "Sraman Mahavira" nga Acharya Mahapragya

"Lord Mahavira dhe kohët e tij" by Kailash Chand Jain (1991) Motilal Banarsidass Publishers PVT LTD Delhi (India)
"Lord Mahavira (Një studim nga perspektiva historike)" by Bool Chand ( 1987 ) P.V. Research Institute I.T.I Road Varanasi 5 (India)
"Lord Mahavira në sytë e të huajve" by Akshaya Kumar Jain ( 1975 ) Meena Bharati New Delhi 110003 (India)

Thënie

"Kur ai u ul [në meditim]... ata i prenë mishin... i shkulën flokët... e ngritën në ajër dhe... e hodhën përtokë... I Nderuari e mërziti dhimbjen." (nga Acaranga Sutra)

Posted in pershkrime

WEBloveDXC

Perpiqu te mose behesh nje njeri i suksesit,por mendoju me mire te behesh nje njeri me vlere.

Menuja kryesore

kerko

Ditari

Link Program

Kombinatorika

Kombinatorika

Historia e kombinatorikës

Kombinatorika numerike

Kombinatorika analitike

Numrat e Fibonaccit

Permutacioni

Numri i permutacioneve

Kombinacioni

Trekëndëshi i Pascalit

Numri i kombinacioneve me përsëritje

Algjebra

Numrat

Numrat real dhe vetitë tyre

Numrat kompleks

Format e numrave kompleks

Mahavira

Lindja e Princit Vardhaman

Vitet e para

Kërkimi shpirtëror

Vitet e mëvonshme

Filozofia

Mahavira

Thënie

Leave a Reply