Newton–Cotes formulas
In numerical analysis, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration (also called quadrature) based on evaluating the integrand at equally-spaced points. They are named after Isaac Newton and Roger Cotes.
Newton–Cotes formulae can be useful if the value of the integrand at equally-spaced points is given. If it is possible to change the points at which the integrand is evaluated, then other methods such as Gaussian quadrature and Clenshaw–Curtis quadrature are probably more suitable.
Contents[hide] |
[edit] Description
It is assumed that the value of a function ƒ defined on [a, b] is known at equally spaced points xi, for i = 0, …, n, where x0 = a and xn = b. There are two types of Newton–Cotes formulae, the "closed" type which uses the function value at all points, and the "open" type which does not use the function values at the endpoints. The closed Newton-Cotes formula of degree n is stated as
where xi = h i + x0, with h (called the step size) equal to (xn − x0) / n = (b − a) / n. The wi are called weights.
As can be seen in the following derivation the weights are derived from the Lagrange basis polynomials. This means they depend only on the xi and not on the function ƒ. Let L(x) be the interpolation polynomial in the Lagrange form for the given data points (x0, ƒ(x0) ), …, (xn, ƒ(xn) ), then
The open Newton–Cotes formula of degree n is stated as
The weights are found in a manner similar to the closed formula.
[edit] Instability for high degree
A Newton–Cotes formula of any degree n can be constructed. However, for large n a Newton–Cotes rule can sometimes suffer from catastrophic Runge's phenomenon where the error grows exponentially for large n. Methods such as Gaussian quadrature and Clenshaw–Curtis quadrature with unequally spaced points (clustered at the endpoints of the integration interval) are stable and much more accurate, and are normally preferred to Newton–Cotes. If these methods can not be used, because the integrand is only given at the fixed equidistributed grid, then Runge's phenomenon can be avoided by using a composite rule, as explained below.
[edit] Closed Newton–Cotes formulae
This table lists some of the Newton–Cotes formulae of the closed type. The notation 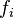 is a shorthand for
is a shorthand for  , with xi = a + i (b − a) / n, and n the degree.
, with xi = a + i (b − a) / n, and n the degree.
| Degree | Common name | Formula | Error term |
|---|---|---|---|
| 1 | Trapezoid rule |  |
 |
| 2 | Simpson's rule |  |
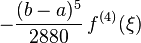 |
| 3 | Simpson's 3/8 rule | 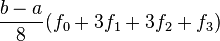 |
 |
| 4 | Boole's rule |  |
 |
Boole's rule is sometimes mistakenly called Bode's rule due to propagation of a typo in Abramowitz and Stegun, an early reference book.[1]
The exponent of the segment size b − a in the error term shows the rate at which the approximation error decreases. The derivative of ƒ in the error term shows which polynomials can be integrated exactly (i.e., with error equal to zero). Note that the derivative of ƒ in the error term increases by 2 for every other rule. The number 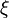 is between a and b.
is between a and b.
[edit] Open Newton–Cotes formulae
This table lists some of the Newton–Cotes formulae of the open type. Again, ƒi is a shorthand for ƒ(xi), with xi = a + i (b − a) / n, and n the degree.
| Common name | step size | Formula | Error term | Degree |
|---|---|---|---|---|
| Rectangle rule, or midpoint rule |
 |
 |
 |
2 |
| Trapezoid method | 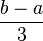 |
 |
 |
3 |
| Milne's rule |  |
 |
 |
4 |
| No name |  |
 |
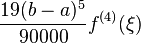 |
5 |
[edit] Composite rules
For the Newton–Cotes rules to be accurate, the step size h needs to be small, which means that the interval of integration ![[a, b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) must be small itself, which is not true most of the time. For this reason, one usually performs numerical integration by splitting
must be small itself, which is not true most of the time. For this reason, one usually performs numerical integration by splitting ![[a, b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) into smaller subintervals, applying a Newton–Cotes rule on each subinterval, and adding up the results. This is called a composite rule, see Numerical integration.
into smaller subintervals, applying a Newton–Cotes rule on each subinterval, and adding up the results. This is called a composite rule, see Numerical integration.
[edit] See also
[edit] References
- M. Abramowitz and I. A. Stegun, eds. Handbook of Mathematical Functions with Formulae, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Section 25.4.)
- George E. Forsythe, Michael A. Malcolm, and Cleve B. Moler. Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977. (See Section 5.1.)
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 4.1. Classical Formulas for Equally Spaced Abscissas", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html?pg=156
- Josef Stoer and Roland Bulirsch. Introduction to Numerical Analysis. New York: Springer-Verlag, 1980. (See Section 3.1.)
[edit] External links
- Hazewinkel, Michiel, ed. (2001), "Newton-Cotes quadrature formula", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/n066510
- Newton–Cotes formulae on www.math-linux.com
- Newton–Cotes Formulae
- Weisstein, Eric W., "Newton-Cotes Formulae" from MathWorld.
- Module for Newton–Cotes Integration, fullerton.edu
- Newton–Cotes Integration, numericalmathematics.com



